计算机组成原理-L03-ALU
本文最后更新于:6 个月前
计算机组成与实践 -算术和逻辑单元(ALU)
一.概述
MIPS指令集:add、sub、and、or……
ALU的实现
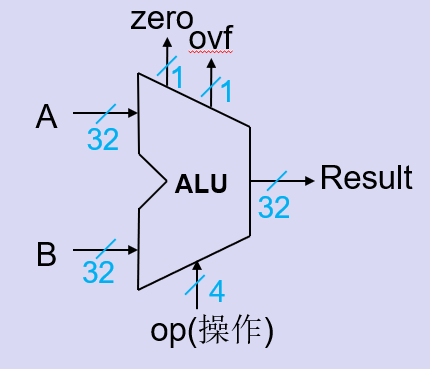
设计MIPS的ALU
必须支持MIPS指令集中的算术与逻辑操作
- 加减指令:add、addi、addiu、sub、subu等
- 乘除指令:mult、multu、div、divu、sqrt
- 逻辑运算指令:and、andi、nor、or、ori、xor
- 分支指令:beq、bne、slt、slti、sltiu、sltu
以及一些指令所需的特殊处理:
- 符号扩展:addi、addiu、slti、sltiu
- 零扩展:andi、ori、xori
- 溢出检测:add、addi、sub
MIPS算术与逻辑指令


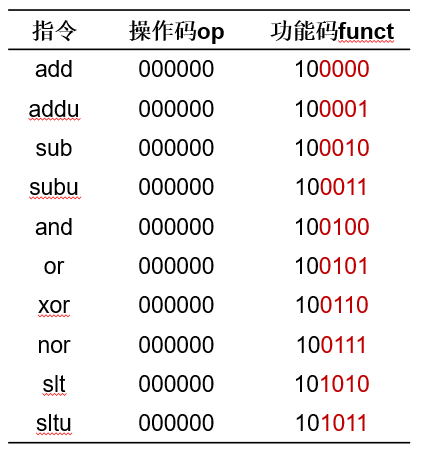
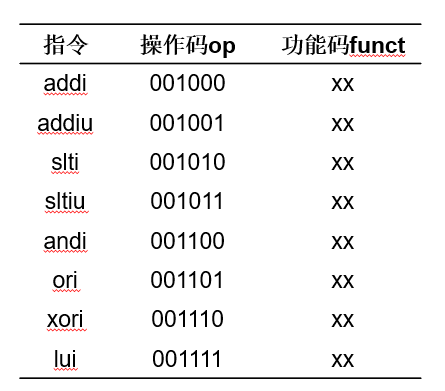
二.加法
加法
7+6
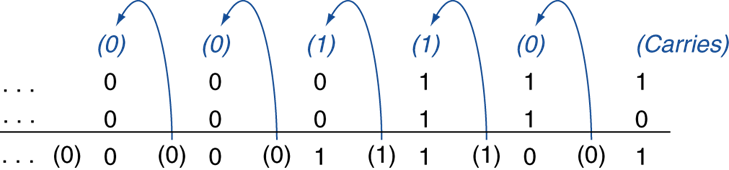
Ø如果结果超过32位将产生溢出
正数和负数相加->不产生溢出
两个正数相加
- 如果结果的符号位为1,则产生了溢出
两个负数相加
- 如果结果的符号位为0,则产生了溢出
1位全加器
Ø输入端:两个加数、进位输入
Ø输出端:和、进位输出
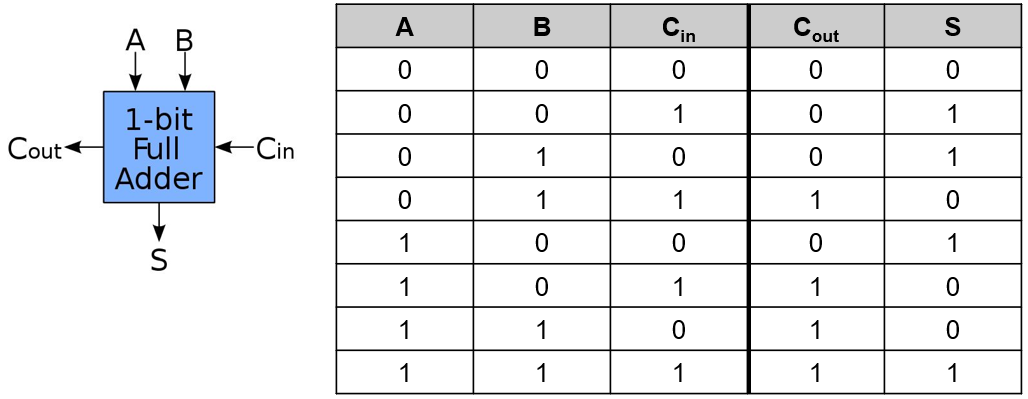
S = A xor B xor Cin
Cout = (A and B) or (A and Cin) or (B andCin)
如何用1位全加器构建32-bit全加器?
:串联32个1位全加器
32-bit全加器
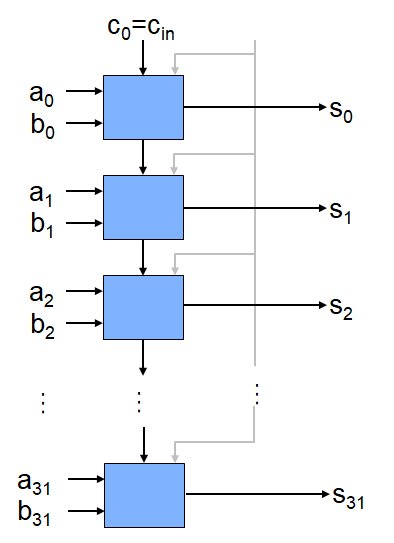
- 将低位的Cout连接到相邻高位的Cin就可以构建32-bit全加器
- 串行加法器或行波进位加法器(Ripple Carry Adder, RCA)
- 🙂:逻辑简单,低开销
- ☹:速度慢
- n-bit串行加法器的性能
- n × CP
快速加法:超前进位
关键是提高高阶进位的速度
Cout = (A and B) or (A and Cin) or (B andCin)
Cout = AB+ACin+BCin= AB+(A+B)Cin
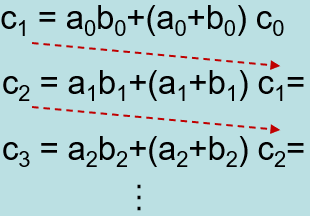
- 进位生成因子(gi): aibi
- 进位传递因子( pi ): (ai+bi)
ci+1 = aibi+ (ai+bi) ci=gi+ pi ci
超前进位
超前进位加法器(carry-lookahead adder)
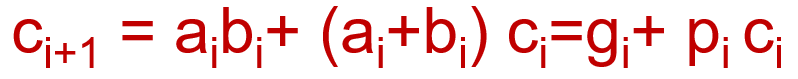
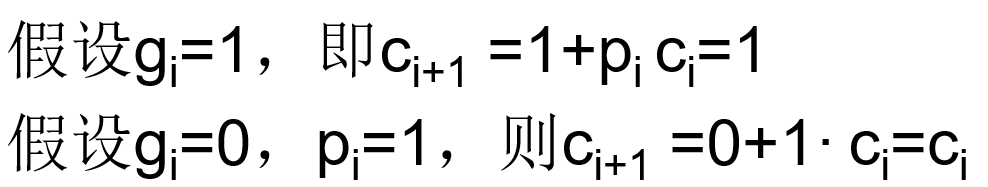
如果之前的加法器生成了一个进位,并且所有的中间传递因子传输了这个进位,那么ci+1 =1
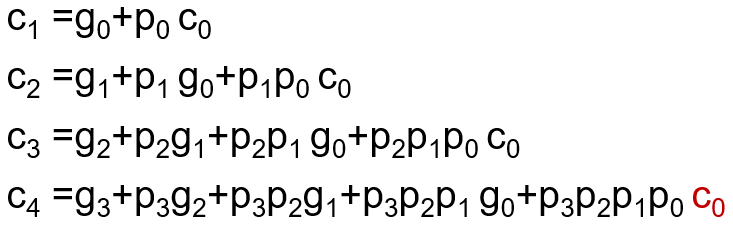
4位并行加法器
根据超前进位设计并行加法器
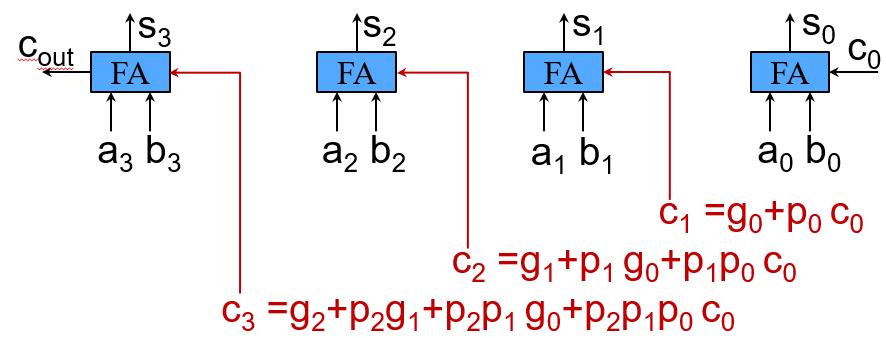
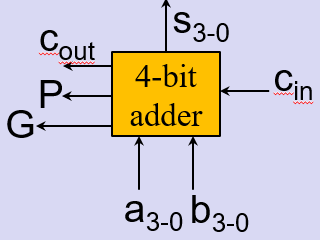
多位并行进位加法器
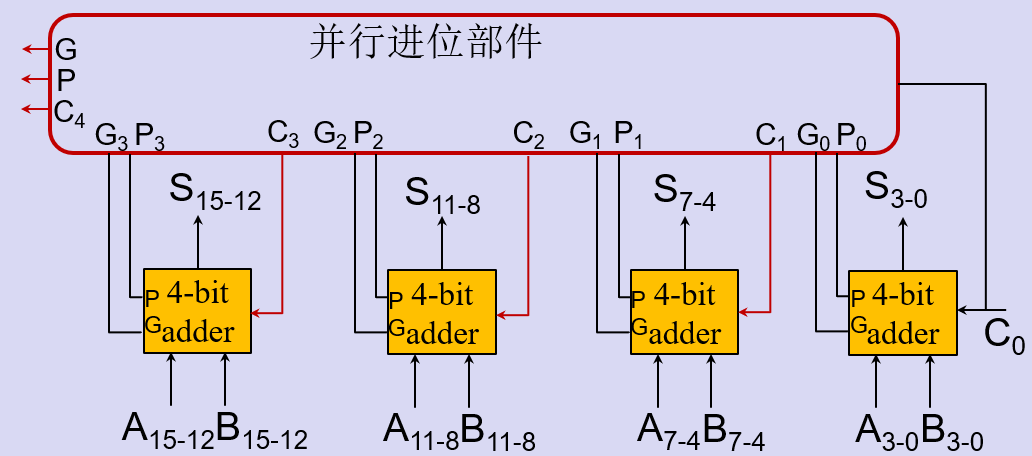

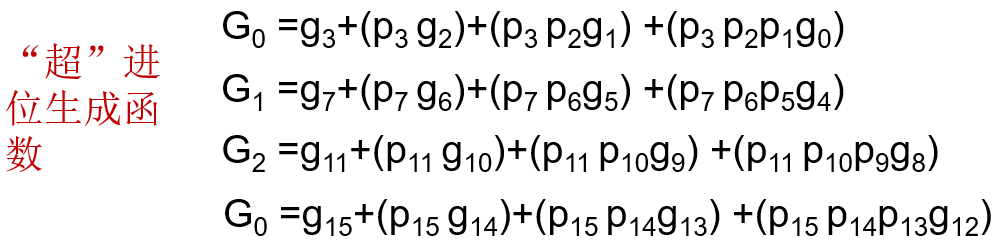
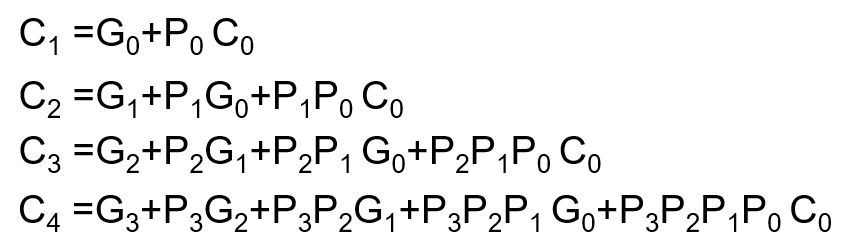
Quiz1-进位传输函数和进位产生函数
- 确定两个16 位数的gi、pi、Pi以及Gi值:
a: 0001 1010 0011 0011–2
b: 1110 0101 1110 1011–2
- CarryOut15(C4)的值是多少
第一题gi,和pi可以直接对应下来计算得出
a: 0001 1010 0011 0011
b: 1110 0101 1110 1011
g: 0000 0000 0010 0011
p:1111 1111 1111 1011
3 2 1 0 Pi 1 1 1 0 Gi 0 0 1 0 第二题,带入
C4=0+0+1+0=1
Quiz2-加法器的性能比较
行波进位加法器和超前进位加法器速度的比较.
假设通过每个与门/或门需要的时间是相同的。比较16 位加法器路径上门延迟的数量,一个用行波进位,另一个用的是两级的超前进位。(1位全加器的每个进位输出信号需要2个门延迟)
行波进位加法器指的将16个1位加法器串联,每个全加器,执行加法的同时执行
S = A xor B xor Cin
Cout = (A and B) or (A and Cin) or (B andCin) 对于这个进位信号,有两种不同的门运算(与和或),门延迟为2,由于串行每一位加法器都需要等待后一个的进位信号,因此从最低进位道最高进位,总门延迟为16*2=32个门延迟
超前进位加法器最高位输出是上一题的C4,由于两级超前进位,每一级内的操作都是并行的,第一步计算小p,小g,都只有一个与或门运算,因此门延迟为1.第二级计算大P,门延迟1,计算大G门延迟2,因此第二级总的门延迟为2(P/G的运算也是并行的).最后计算C4时的门延迟为2。整体最坏的门延迟是5(假设每个逻辑运算都是一个门延迟).
减法
看作加法的第二个操作数为负数

减法器设计
设计思想:X – Y = X + (-Y)
- 每个bit位取反
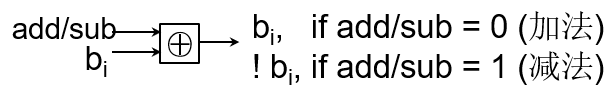
- 最低位加1
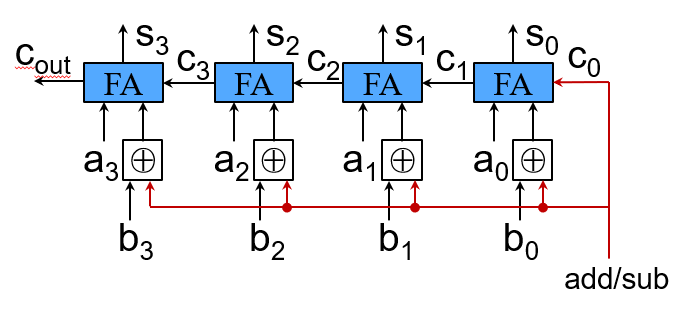
感觉是取模得到最高位(符号位)然后再按不同的方法处理
溢出检测
如果结果超过32位将产生溢出
- 两个正数或两个负数相减,不产生溢出
- 当正数加正数:结果符号位为1则溢出
- 当负数加负数:结果符号位为0则溢出
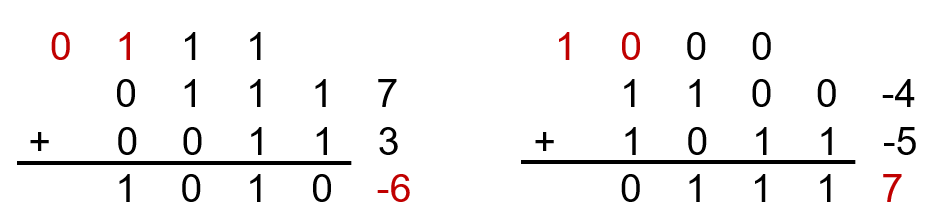
- 最高有效位的进位输入与进位输出异或
V=Cin ⊕ Cout
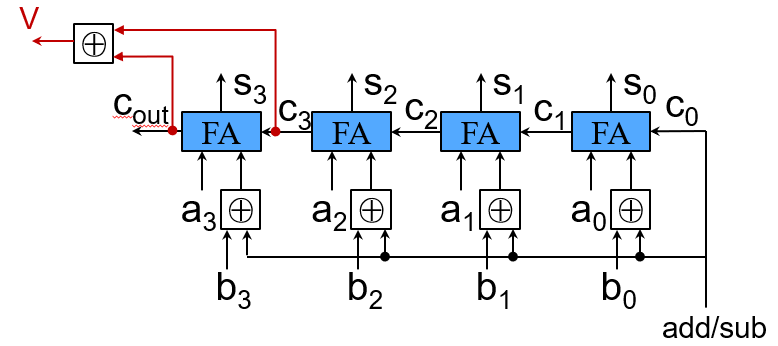
- 无符号整数的溢出可以忽略
- 溢出时产生异常
- 加法add、立即数加法addi 和减法sub
- 溢出时不产生异常
- 无符号加法addu、立即数无符号加法addiu 和无符号减法subu
- C语言忽略溢出,C编译器采用无符号算术指令
ALU需要支持的其他操作
- 逻辑操作(and, or, xor, nor)
- 按位操作,不涉及进位
- 每个功能需要一个逻辑门,多选器选择输出结果
- 小于则置位指令(slt)
- 使用减法判断a-b是否小于0
- 条件分支指令的相等测试(bne,beq)
- 使用减法判断a-b是否等于0
- 立即数指令
- ALU外设置符号扩展
支持逻辑操作的ALU单元设计
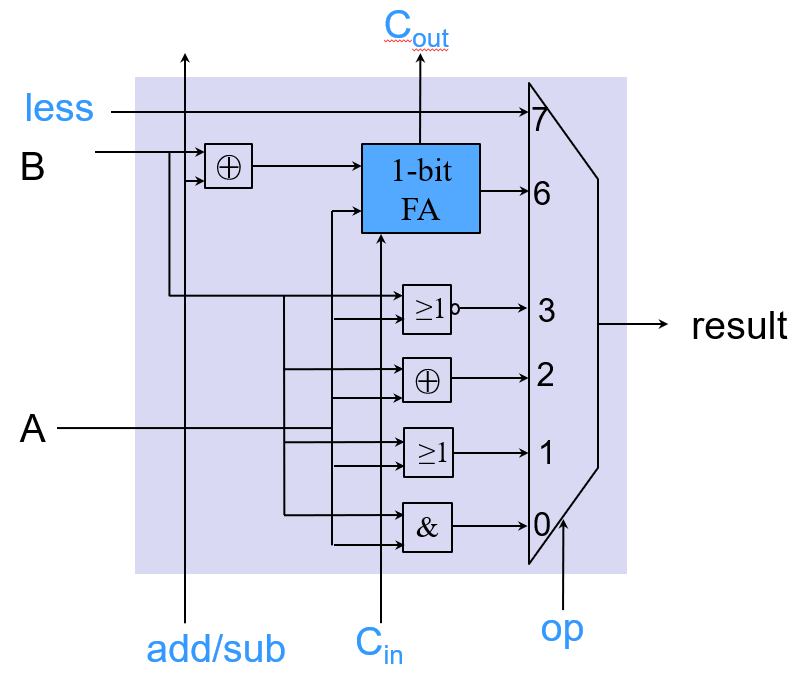
实现slt
- 首先进行减法
- 如果减法结果为负数(最高有效位结果为1),将result置为1
- 如果减法结果为正数(最高有效位结果为0),将result置为0
- 将最高有效位(set)连接到最低位的less输入
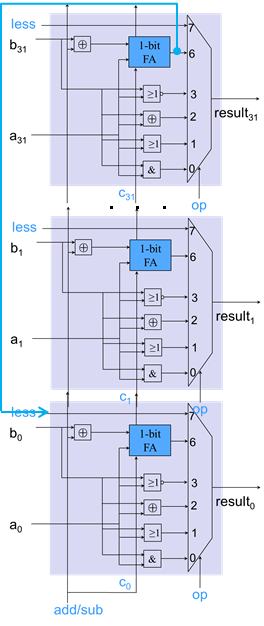
一个简单完整的ALU
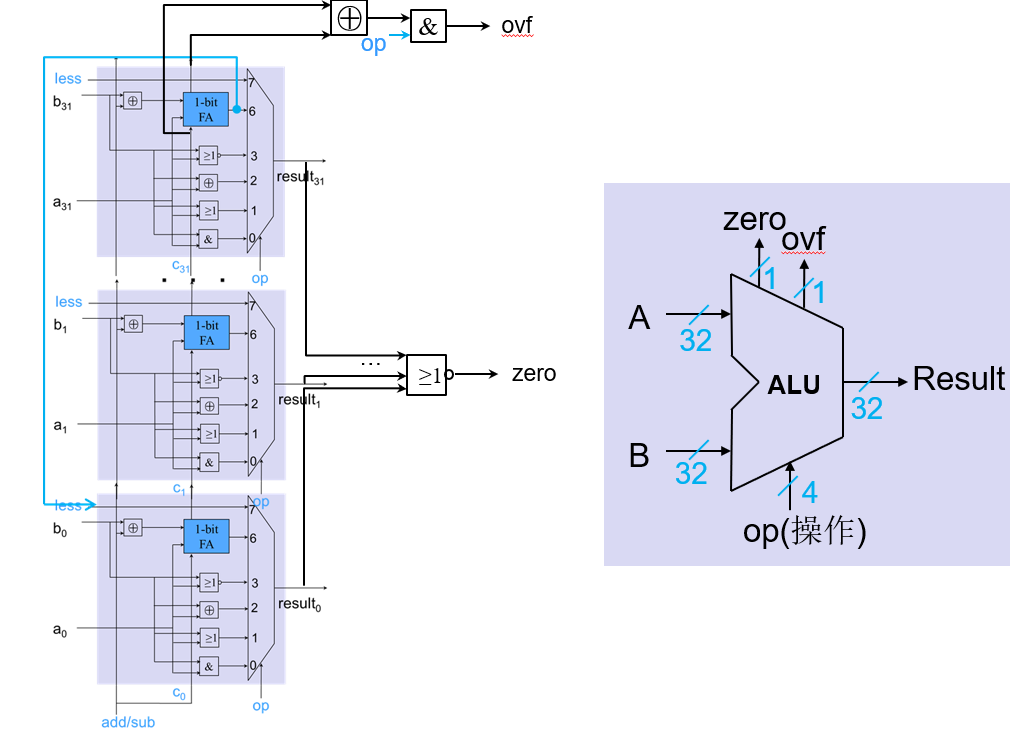
三.乘法和除法
乘法
通过移位与加法实现
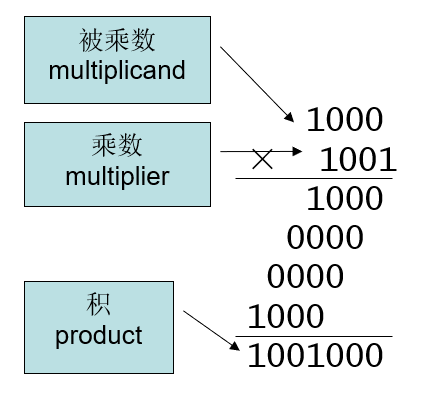
积的位数是被乘数与乘数的位数之和
乘法的硬件实现(第一版)
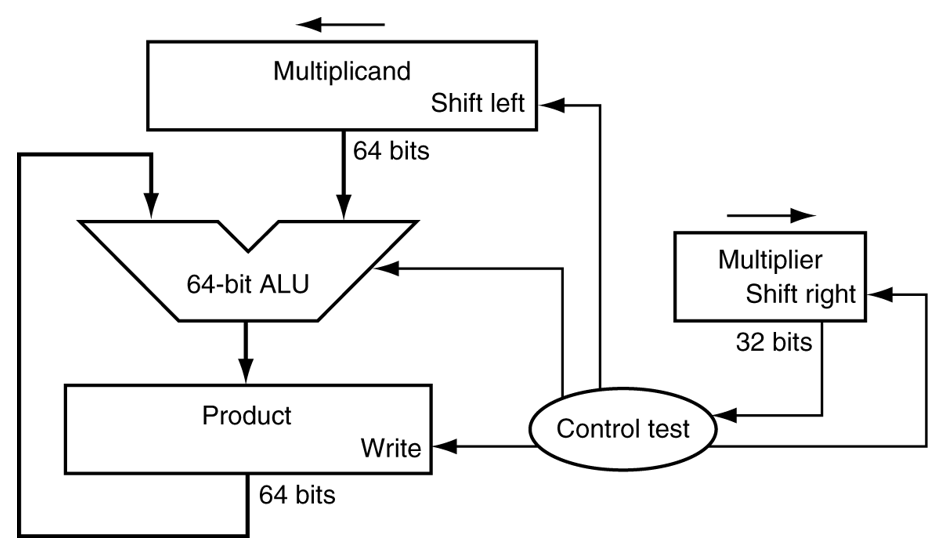
硬件:
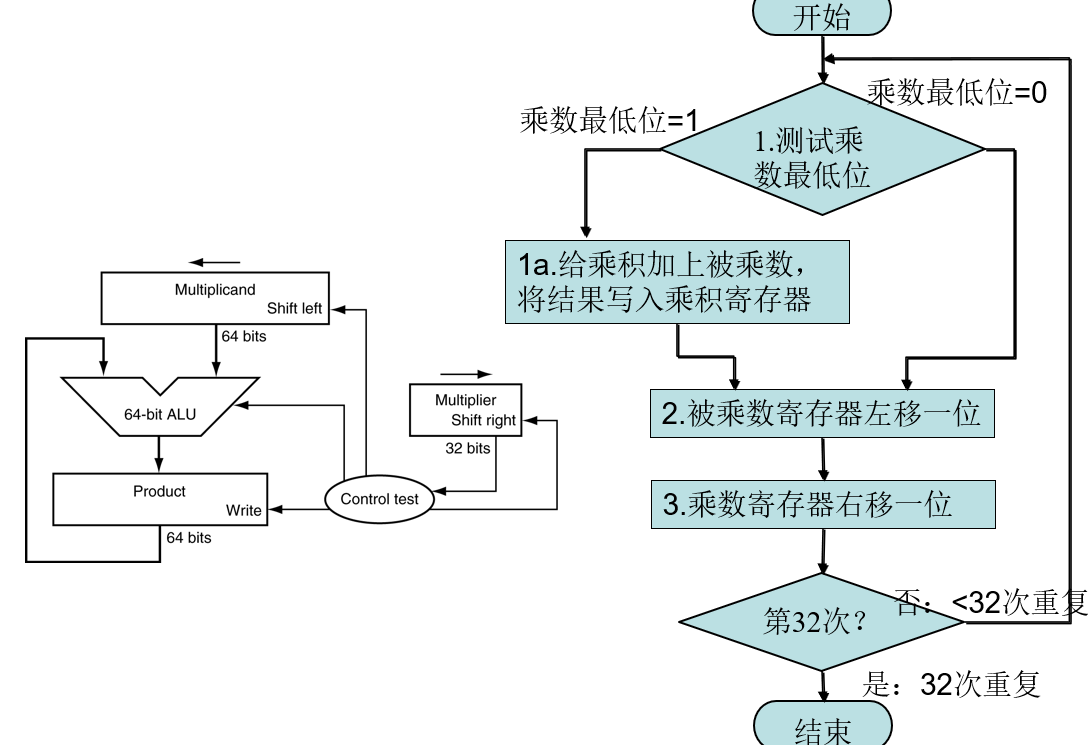
改进后的乘法器
同时进行加法和移位
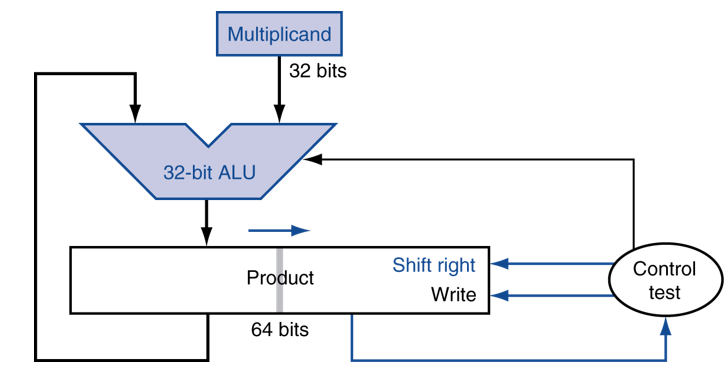
每一步只需要一个时钟周期
乘法运算频率较低时
例子-1
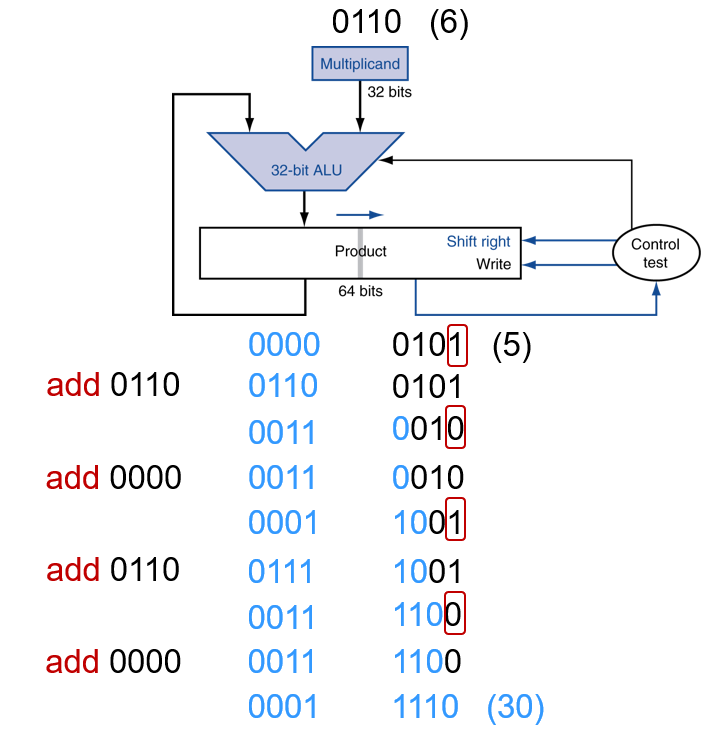
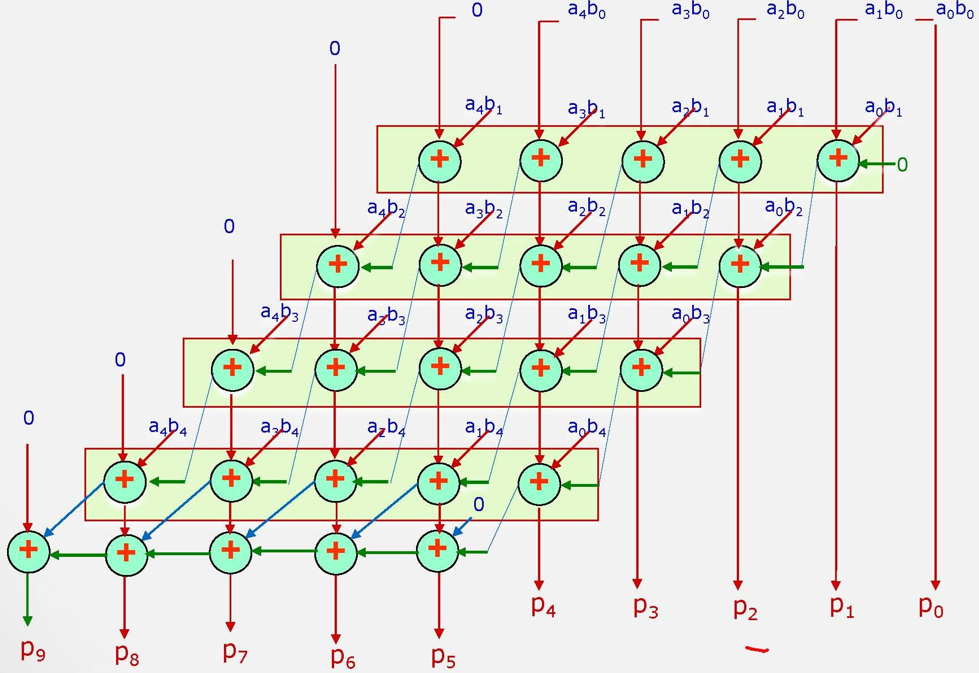
更快速的乘法

更快速的乘法器设计
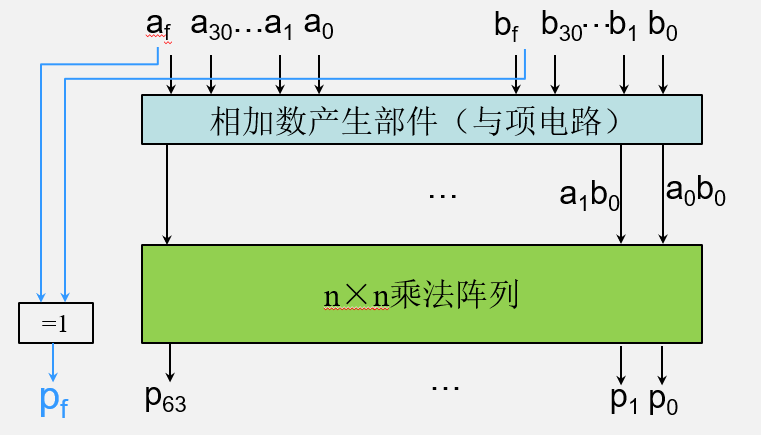
n×n乘法阵列
MIPS中的乘法指令
乘法mult和无符号乘法multu
1 | |

一对容纳64位乘积的寄存器:$hi和$lo
- 高32-bit放入寄存器hi,低32-bit放入寄存器lo
- 用于存储乘法与除法的结果
- 不可直接寻址访问
- 通过mflo(move from lo)和mfhi(move from hi)两个指令将积送入指定的寄存器
编译器会用移位指令替代乘数为2的幂次的乘法操作
除法
- 除数不能为0
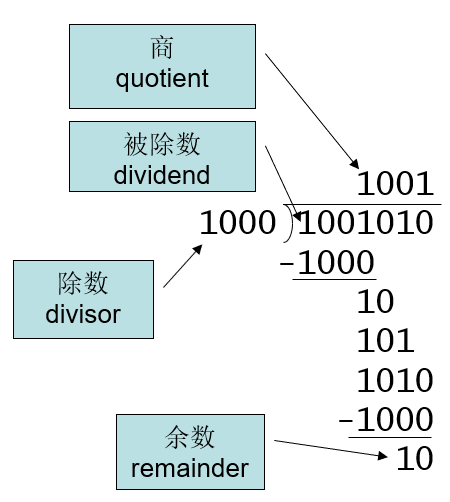
- 长除法
- 如果除数<=被除数
- 该位商为1,被除数减去除数
- 其他
- 该位商为0,取被除数下一位
- 可恢复的除法
- 被除数减去除数,直到余数小于0,再将被除数加回来
- 有符号除法
- 采用绝对值进行除法
- 源操作数的符号相反时商为负,同时使非零余数的符号和被除数的相同
除法的硬件
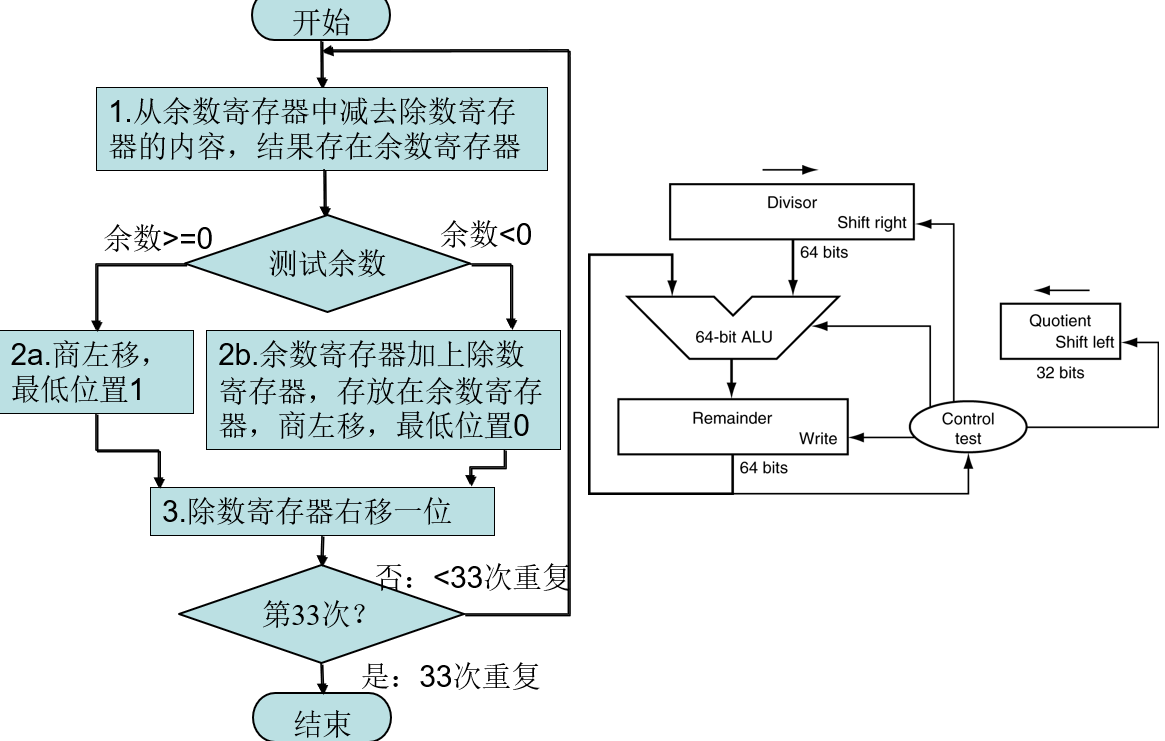
改进后的除法器
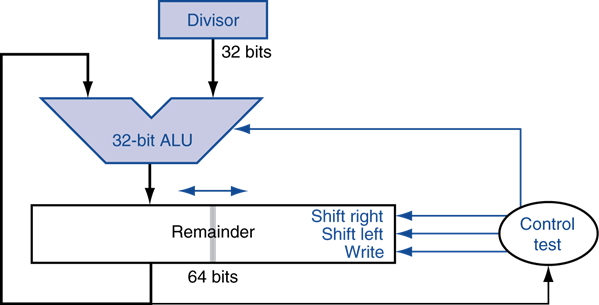
将加法器和寄存器的位长减半
将加法器和寄存器的位长减半
有些部件可以共用
MIPS中的除法
除法div和无符号除divu
1 | |
- R型指令格式
- 乘法和除法共用硬件
- 商存放在$lo,余数存放在$hi
- 采用mflo和mfhi指令将运算结果放入其他寄存器
四.移位
移位操作
将所有位向左或者向右移动
1 | |

- 5bit移位域足够表示移动31位
- 逻辑移位以0填充,算术移位以符号位填充
- 移位与ALU分开实现
- 空指令(nop)当作特殊的左移指令
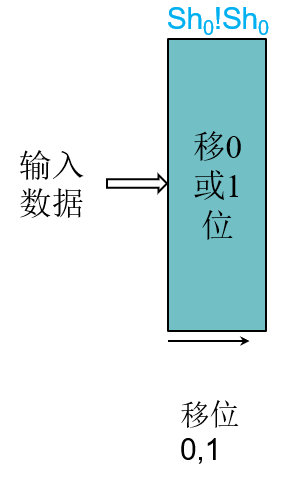
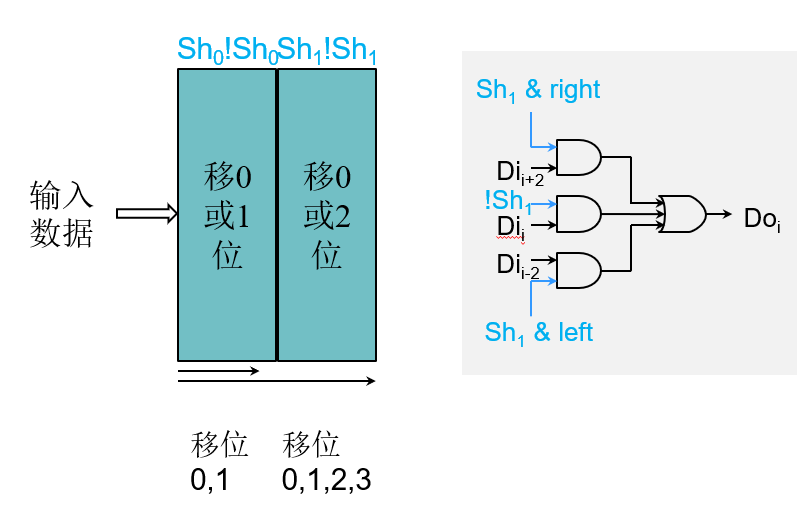
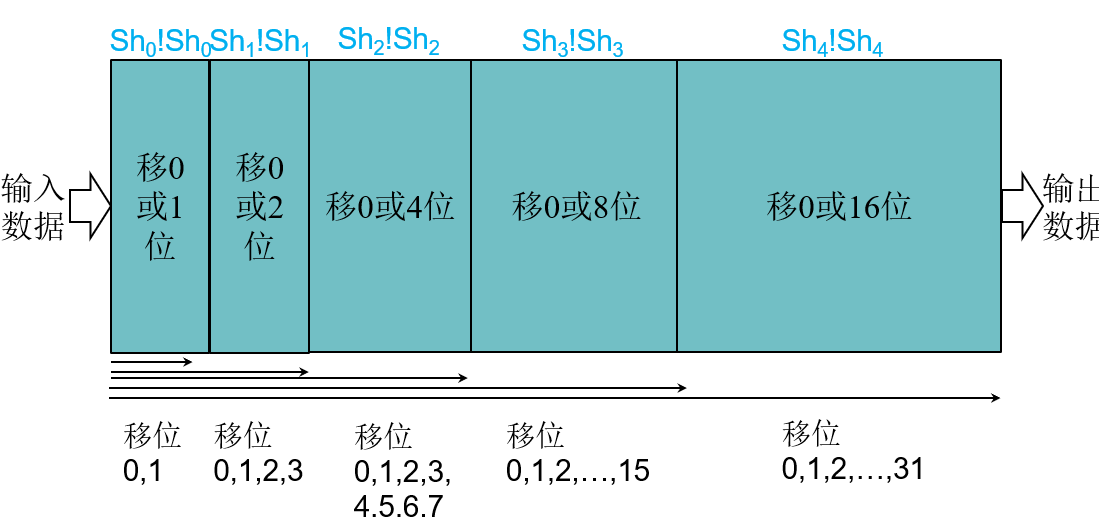
移位单元
控制:
- 移动距离(Sh4Sh3Sh2Sh1Sh0)
- 移动方向(left,right)
- 移动类型(逻辑logical,算术arithmetic)
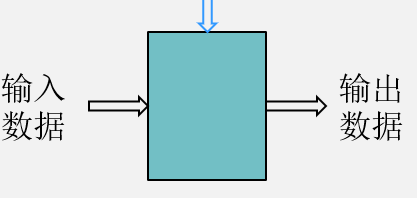
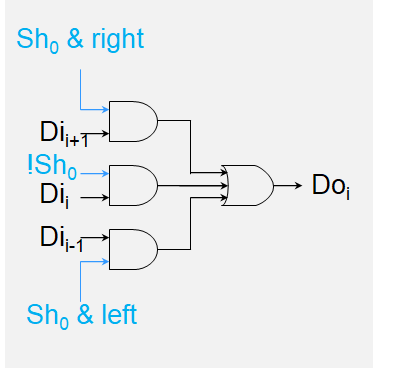
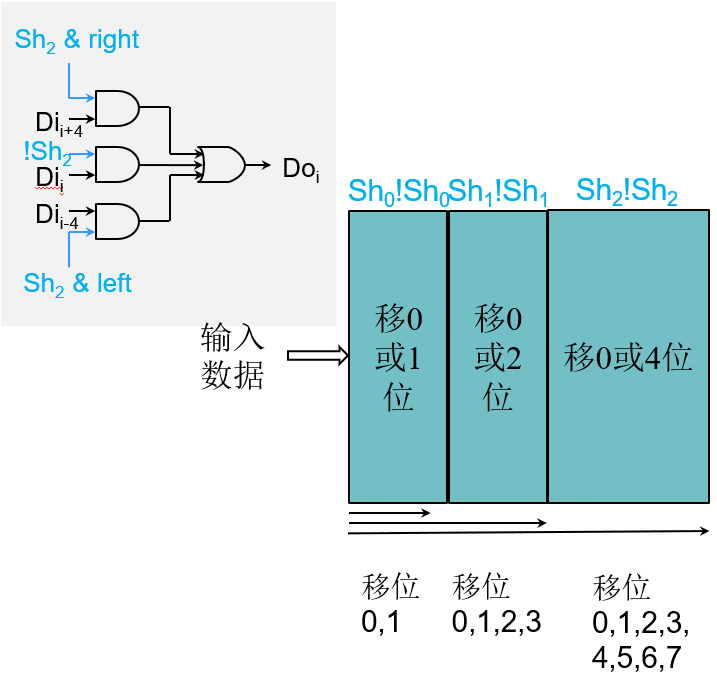
移位实现
| Sh0 | !Sh0 | r | l | Doi |
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | Dii+1 |
| 1 | 0 | 0 | 1 | Dii-1 |
| 0 | 1 | 0 | 0 | Dii |
五.浮点数
计算机中以浮点数表示实数
科学计数法
–2.34 × 10^56
+0.002× 10^–4
+987.0210 × 10^9
| 规格化(Normalized)数 |
|---|
| 一个采用科学记数法表示的数,若没有前导零且小数点左边只有一位整数 |
浮点数
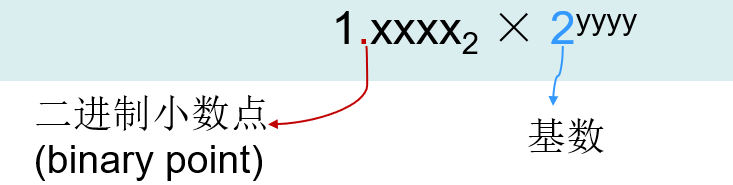
| 浮点数(floating point) |
|---|
| 二进制小数点不固定的表达数的计数法 |
- 简化了浮点数的数据交换
- 简化了浮点数的算术算法
- 提高了用一个字存储的数的精度
IEEE754浮点数格式
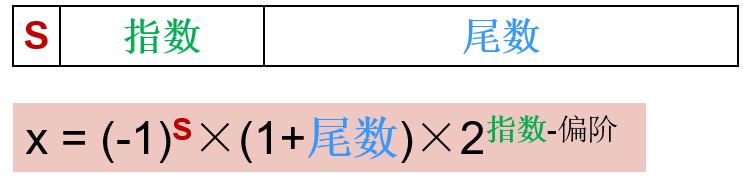
- S:符号位(0 Þ非负,1 Þ负)
- 规格化计数:1.0<=|有效位|<=2.0
- 二进制数的前导位为1,不需要表示
- 有效位由1.与后面的尾数部分构成
- 指数:实际的指数+偏阶
- 指数为无符号数,为了表示2^-126到2^-127采用了偏阶
- 单精度偏阶为127,双精度偏阶为1023
- 指数代表数值范围,尾数代表数的精度,指数域和尾数域大小需要折中
单精度浮点数的取值范围

- 指数00000000和11111111是保留值(1~254)
- 最小的值
- 指数为00000001 -> 实际指数= 1 – 127 = –126
- 尾数:000…0 -> 有效位 = 1.0
- ±1.0 × 2^–126 ≈ ±1.2 × 10^–38
- 最大的值
- 指数:11111110 ->实际指数= 254 – 127 = +127
- 尾数:111…1->有效位 ≈ 2.0
- ±2.0 × 2^+127 ≈ ±3.4 × 10^+38
双精度浮点数的取值范围

- 指数000…0到111…1是保留值(1~2046)
- 最小的值
- 指数为00000000001 -> 实际指数= 1 – 1023 = –1022
- 尾数:000…0 -> 有效位 = 1.0
- ±1.0 × 2^–1022 ≈ ±2.2 × 10^–308
- 最大的值
- 指数:11111111110 -> 实际指数= 2046-1023= +1023
- 尾数:111…1-> 有效位 ≈ 2.0
- ±2.0 × 2+1023 ≈ ±1.8 × 10^+308
溢出
浮点数表示法可以表示很大的数值范围,但与无穷还是不同
溢出(上溢):正的指数太大而超过指数域的表示范围
下溢:负的指数太小而超过指数域的表示范围
浮点数=>异常
浮点数的精确度
- 相对精确度
- 所有尾数位是有效位
- 单精度:约2–23
- 23 × log102 ≈ 23 × 0.3 ≈ 6 位十进制的精度
- 双精度:约2–52
- 52 × log102 ≈ 52 × 0.3 ≈ 16 位十进制的精度
浮点数例子1

浮点数例子2

特殊数
| 单精度 | 双精度 | 表示对象 | ||
|---|---|---|---|---|
| 指数 | 尾数 | 指数 | 尾数 | |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 非0 | 0 | 非0 | ±非规格化数 |
| 1~254 | 任何值 | 1~2046 | 任何值 | ±浮点数 |
| 255 | 0 | 2047 | 0 | ±无穷 |
| 255 | 非0 | 255 | 非0 | NaN(非数) |
- ±无穷
- 避免溢出检测的需要
- 非数(Not-a-Number,NaN)
- 表示非法数或者无效操作结果
- e.g., 0.0 / 0.0
浮点数加法


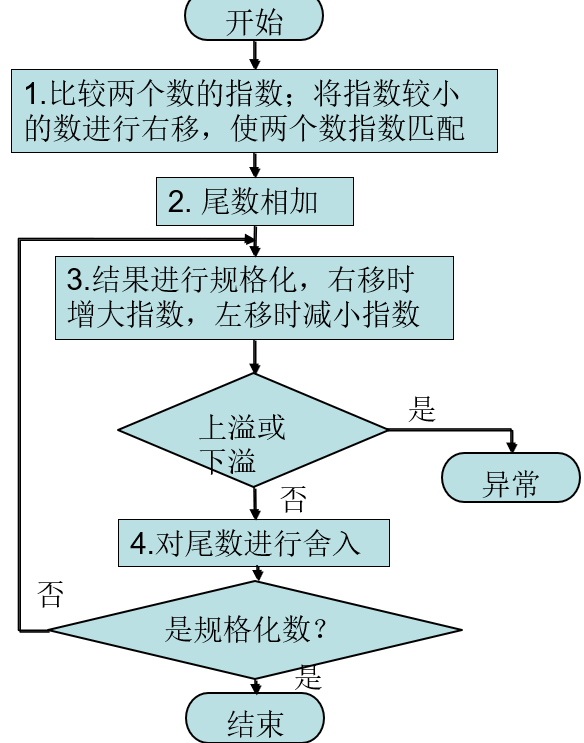
FP加法器
- 比整数加法器复杂
- 如果采用单周期时间完成,时钟周期很长
- 比整数操作时间长很多
- 较慢的时钟周期将会影响所有指令
- FP加法器花费几个时钟周期
- 可以并行执行
浮点加的基本结构
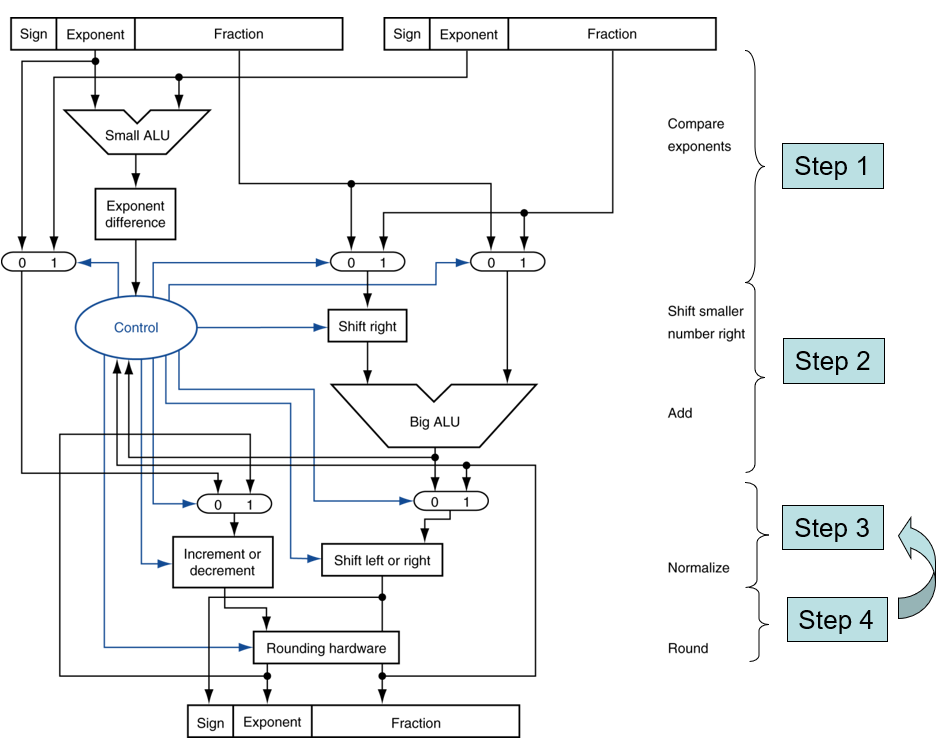
浮点数乘法


FP运算的硬件
- FP乘法器与FP加法器相似
- 对有效数采用乘法,而不是加法
- FP运算硬件通常可以实现
- 加法,减法,乘法,除法,倒数,平方根
- FP操作花费几个时钟周期
- 并行执行
MIPS中的浮点指令
- 浮点寄存器
- MIPS 设计增加了单独的浮点寄存器——称为$f0,$f1,$f2 ,…,$f31
- 双精度寄存器是一组单精度寄存器的偶数-奇数对,并使用偶数寄存器编号作为其名称
- 针对浮点寄存器的存和取指令: lwcl 和swcl
- 单精度指令
- add.s, sub.s, mul.s, div.s, c.x.s(例如c.eq.s)
- 双精度指令
- add.d, sub.d, mul.d, div.d, c.x.d(例如c.eq.d)
- 浮点比较为真跳转bclt 和浮点比较为假跳转bclf
浮点数例子:°F转°C
C 代码:
1 | |
MIPS汇编代码:
1 | |
浮点数例子:矩阵乘法
C = C + A × B
都是32 × 32 的二维矩阵, 每个元素都是双精度
C 代码:
1 | |
a,b,c的基地址是参数,存在$a0,$a1,$a2中,i, j, k 分别存在$s0,$s1,$s2中。
1 | |
算术精确性
- IEEE 756提供几种舍入模式
- 中间结果总是多保留两位,称为保护位(guard)和舍入位(round)
- 四种舍入模式: 总是向上舍入(向+∞ ),总是向下舍入(向- ∞ ) , 截断舍入,向最靠近的偶数舍入。
- 例子:2.56 × 10^0 与 2.34 × 10^2相加
- 首先右移较小的数以对齐指数,有了保护位和舍入位,可以表示两个最低位:0.0256+2.3400=2.3656 (×10^2),
- 舍入后变为2.37 ×10^2
- 如果没有保护位和舍入位:0.02+2.34=2.36 (×10^2)
六.小结
- 位模式没有内在的含义
- 对位模式的操作决定其含义
- 计算机中的数字
- 有限的数值范围与精度
- 程序设计中需要考虑到
- 体系结构支持的算术运算
- 有符号与无符号整数运算
- 以浮点数近似表示的实数的运算
- 有限的取值范围与精度
- 运算可能出现上溢或者下溢